Contents
There are several basic concepts of photography that are essential to know before you start shooting your own photos. Without knowing the terms and definitions you can’t get the best out of your camera. You won’t need to know them to shoot photos in a full automatic mode (Samsung: “SMART”), but it is useful to understand them in case you want to use the more flexible modes like Aperture priority (A), Shutter priority (S), manual mode (M).
This introduction will introduce the terms focal length, exposure, aperture, depth of field, shutter speed, ISO sensitivity and exposure value (compensation).
Focal length
The focal length is basically the distance between a single optical lens and the focal point, where the light rays meet each other. This is not necessarily the length of the camera’s lens nowadays. In the end the focal length directly influences the picture detail. The greater the focal length the narrower the angle of view and the picture detail. In other words: Increasing the focal length increases the magnification.
| Example 1: | |
Aperture & Depth of field
The aperture is a hole through which light travels and which controls the amount of light that enters the camera. The lenses usually contain several thin plates that can be opened or closed which changes the size of the aperture and therefore the amount of light. The impact on the photo is shown in the brightness and the depth of field (see below). The maximum aperture is used when the aperture is completely opened and the minimum aperture is used when the smallest hole is chosen.
| Example 2: | ||
|
|
|
|
The different possible sizes of the aperture are usually “named” using a formula / a numerical representation. This is called the “F-Number“, or “lens speed”. The f-number represents the focal length divided by the diameter of the lens: 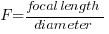 . For example, the NX lens Samsung 30mm f/2.0 has a focal length of 30mm and a f-number of 2.0. Using the formula we can calculate the diameter of the aperture:
. For example, the NX lens Samsung 30mm f/2.0 has a focal length of 30mm and a f-number of 2.0. Using the formula we can calculate the diameter of the aperture:  . The f-number has different used notations, e.g. f/2.8, F2.8 or 1:2.8. On zoom lenses the maximum aperture can depend on the focal length, e.g. a “normal” kit lens like the Samsung 18-55mm f/3.5-5.6 has a f-number of 3.5 for the focal length of 18mm and 5.6 for 55mm respectively.
. The f-number has different used notations, e.g. f/2.8, F2.8 or 1:2.8. On zoom lenses the maximum aperture can depend on the focal length, e.g. a “normal” kit lens like the Samsung 18-55mm f/3.5-5.6 has a f-number of 3.5 for the focal length of 18mm and 5.6 for 55mm respectively.
The wider the aperture is (namely the lower the aperture value), the lower the depth of field (DOF) becomes. The depth of field is the distance between the nearest and the farthest objects in a scene that appear sharp in the photo. The more away objects are from the point you focussed on the more blurred the objects are.
| Example 3: | |
However, the depth of field is not only affected by the aperture, it depends on three things:
- Aperture
A low aperture value leads to a photo with a low depth of field (see example 3). - Focal length
The longer the focal length is, the lower the depth of field gets (see example 1). - Distance between the subject and the camera
The shorter the distance between the subject and the camera is, the lower the depth of field gets.
Shutter speed
Shutter speed is the name describing the time the shutter is opened to take a picture. Like the aperture it controls the brightness of a photo. A faster shutter speed means less light is entering the lens and vice versa. A low/fast shutter speed, e.g.  , tends to freeze motions. This can be useful when shooting fast moving objects like athletes, driving cars or running water. A high/slow shutter speed, e.g. 2 seconds, usually leads to blurred photos, but might be useful in dark situation or to avoid the the “freezing effect” for running water.
, tends to freeze motions. This can be useful when shooting fast moving objects like athletes, driving cars or running water. A high/slow shutter speed, e.g. 2 seconds, usually leads to blurred photos, but might be useful in dark situation or to avoid the the “freezing effect” for running water.
| Example 4: | |
ISO sensitivity
The sensor can be set to different levels of sensitivity. To express the sensitivity there are several norms, e.g. ASA and ISO. ISO is currently the most frequently used way for the sensitivity and it is also used by Samsung cameras. ISO sensitivity is expressed using numbers, like ISO 100, which is usually the lowest ISO number you can choose. The highest ISO sensitivity is defined by the camera manufacturer and depends on the capabilities of the sensor used in the camera. An example for a high ISO sensitivity is 6400 nowadays, but this changes as sensors evolve.
The lower the ISO sensitivity is the more light you need to expose the photo properly. The problem with higher ISO sensitivity is that image noise increases which leads to a decreased image quality.
| Example 5: | |
|
|
|
A really good explenation about ISO sensitivity can be found on YouTube. Dylan Bennet did a great job in explaining ISO:
Exposure
The combination of the shutter speed, the aperture and the luminance of a subject determine the amount of light that reaches the sensor. This is called the exposure.
For each photo you need to think about the settings you should use to get the best result. Think about the available light, the desired depth of field and the movement of the objects you want to photograph (and don’t forget the “movement” of the camera itself). Afterwards you need to choose the best combination respectively a reasonable compromise of aperture, shutter speed and ISO sensitivity to get a proper exposure of your photos.
Exposure value (compensation)
The exposure value (EV) is a quantity that incorporates the shutter speed and the aperture. Below is a table which gives you the exposure values of different aperture and shutter speed combinations using ISO 100.
| EV |  |  |  |  |  |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f/32 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| f/22 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| f/16 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| f/11 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| f/8 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| f/5.6 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| f/4 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| f/2.8 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| f/2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| f/1.4 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
The more light the lower the number. The amount of light is the same for all combinations with the same number. For example, choosing 1s and f/16 gives you the same amount of light as choosing 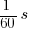 and f/2.
and f/2.
Many modern cameras, including all Samsung NX cameras, have a setting called exposure (value) compensation. You can select different options in steps of 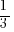 (other cameras may also allow steps of
(other cameras may also allow steps of 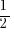 ). 0 is the default value which is the normal exposure the camera is suggesting to use. -1 means you only get half of the light, +1 means you get the double of the light. These -1/+1 steps are also called “stops”, you could say changing the shutter speed from 1s to 2s is an exposure compensation of plus one or you could simply say we gained one stop.
). 0 is the default value which is the normal exposure the camera is suggesting to use. -1 means you only get half of the light, +1 means you get the double of the light. These -1/+1 steps are also called “stops”, you could say changing the shutter speed from 1s to 2s is an exposure compensation of plus one or you could simply say we gained one stop.
To give you an idea what one stop is, here are lists with values that are separated by one stop each:
- ISO: …, 100, 200, 400, 800, 1600, 3200, … (EV +/-1 doubles/halves the ISO value)
- Aperture: …, 1.4, 2.0, 2.8, 4, 5.6, 8, 11, 16, 22, 32, …
- Shutter speed: …,
 ,
, 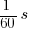 ,
, 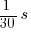 ,
, 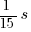 ,
, 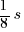 ,
,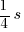 ,
,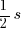 ,
,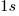 ,
,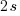 ,
, 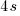 , … (EV +/-1 doubles/halves the time [approximated])
, … (EV +/-1 doubles/halves the time [approximated])
Link Tip
I found a tool from Canon which allows you to play around with the settings described above. You can see what effect the adjustment of those settings have on the final photo. It’s made by Canon but this is also a very good tool for Samsung users, too. 🙂 Visit www.canonoutsideofauto.ca/play.












Good stuff
Thanks….
Hi Matt,
I think the chart works the other way around, doesn’t it ? You wrote “The more light the higher the number”, I think it is the other way around. 2 seconds at f1.4 is definitely the highest amount of light in your chart, and the number is 0, so it should be “The more light the lower the number” ;o)
Cheers.
Jay
Hi Jay,
you are absolutely right. Thank you for pointing that out. I’ll correct that!
Cheers, Matt
Hello Matt, great article, there are several errors on the post though for some reason.
(“Error: https://matteverglade.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/ must have write access Read the official wpmathpub plugin FAQ for more details”
Any chance you could take a look and correct?
Has been fixed, not sure why it broke.
Detailed photography concept. Like the stuff.
Here the information you included is very important to match the area of focus, besides we will be very happy if you regular set up like this post. Thanks in advance!!